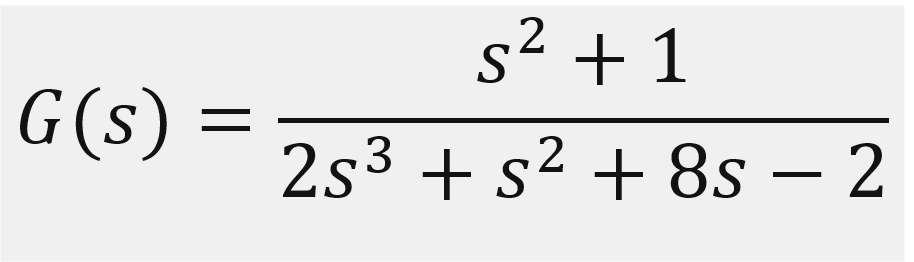Matlab y Aplicaciones
Los cursos no son obligatorios, puesto que las cápsulas aportan lo necesario para aprender Matlab y Simulink. Sin embargo, existen contenidos más específicos que son únicos de los cursos y viceversa, por lo que se recomienda explorar ambos.
Julián Retamal Márquez, Ing. civil eléctrica



Binomial
Ejemplo: Cierto método de control tiene una efectividad de un 88%. Calcular la probabilidad de que para 80 plantas, más de 70 sean controladas de manera efectiva.
Solución: Se tiene que n=80, k=70 y p=0.88, por lo que se escribe en Matlab:
>> P=binomial (80,70,0.88)
Presionando enter se entregan cinco opciones:
1. x=70
2. x<70
3. x<=70
4. x>70
5. x>=70
Como se buscan más de 70 éxitos, se escribe la opción 4 y luego enter, donde se obtiene lo siguiente:
Recomendación: Estar cursando o tener aprobada la asignatura “Probabilidades y estadísticas para la ingeniería”.
Carreras: Cualquier ingeniería civil.
Normal
Ejemplo: Cierto transformador opera a una potencia aparente media de 2[Kva], con una desviación estándar de 0.32 [Kva]. Calcular la probabilidad de que trabaje a una potencia menor a 1.88 [Kva] si éste se modela con distribución normal.
Solución: u = 2, a=0.32 y x=1.88, por lo que se ingresa la función
>> P=normal (2, 0.32, 1.88)
Donde se esntregan las siguientes opciones:
1. x<1.88
2. x>1.88
Por lo que ingresando la opción 1, se tiene que P = 0.358.
1
P =
0.3538
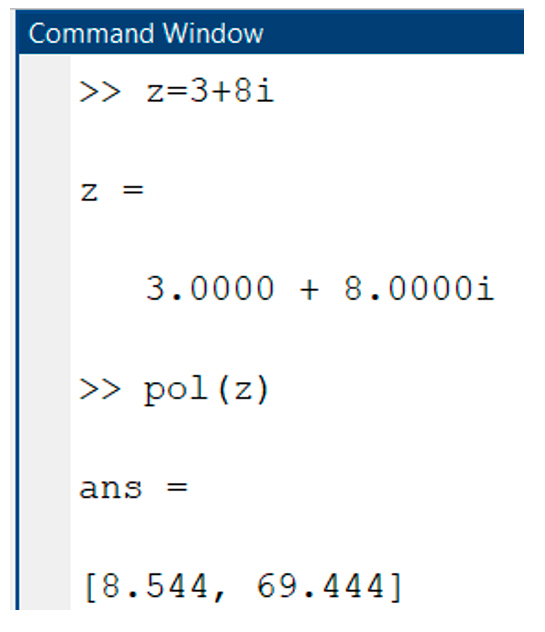
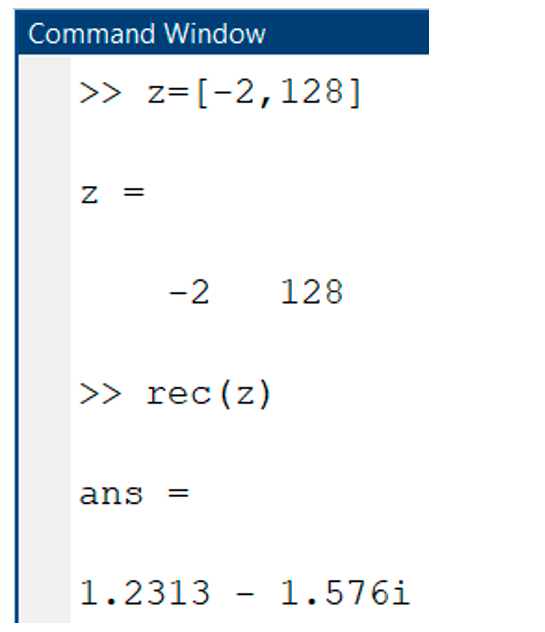
pol y rec
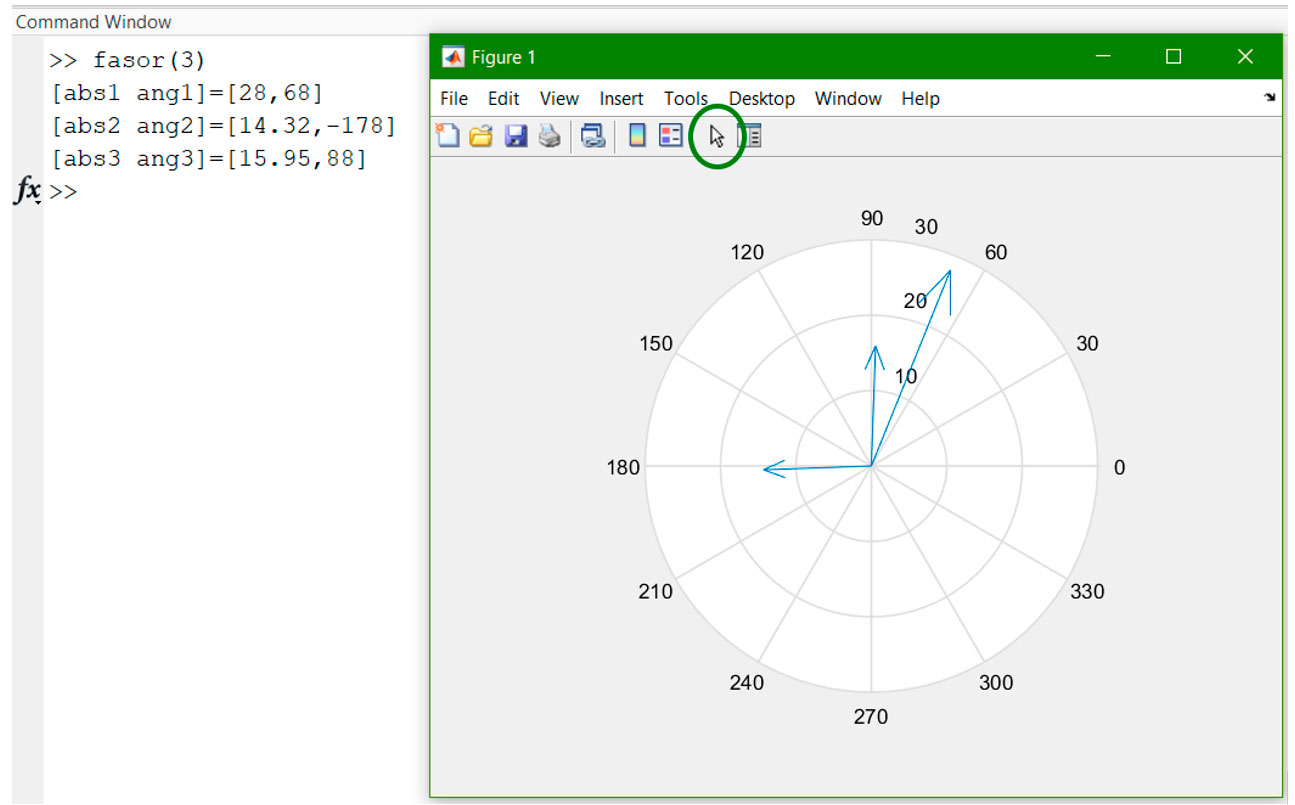
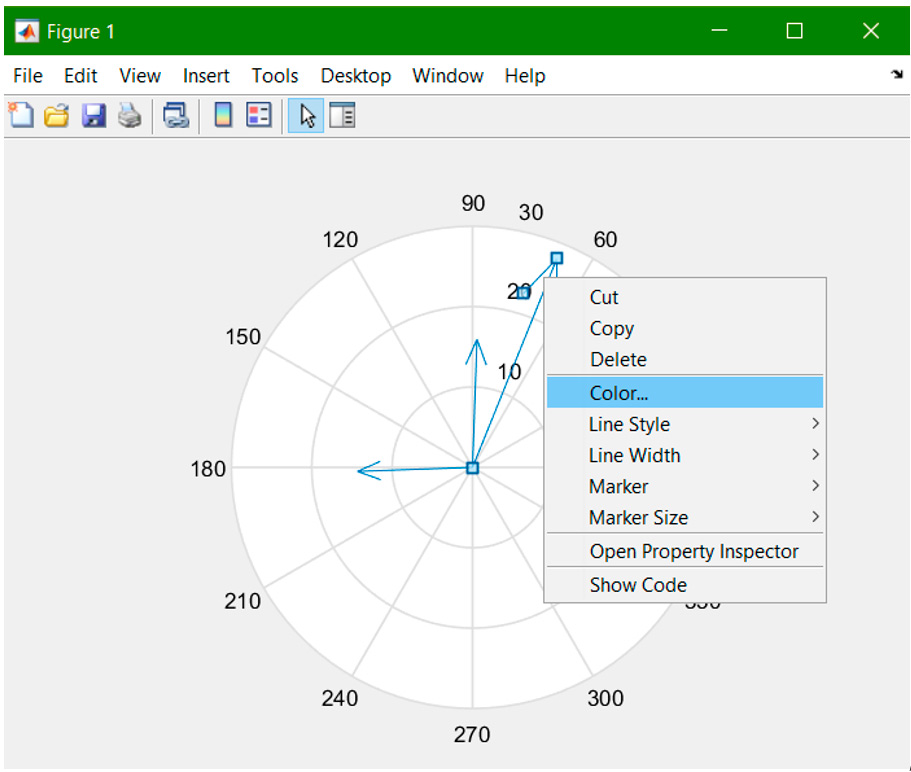
fasor
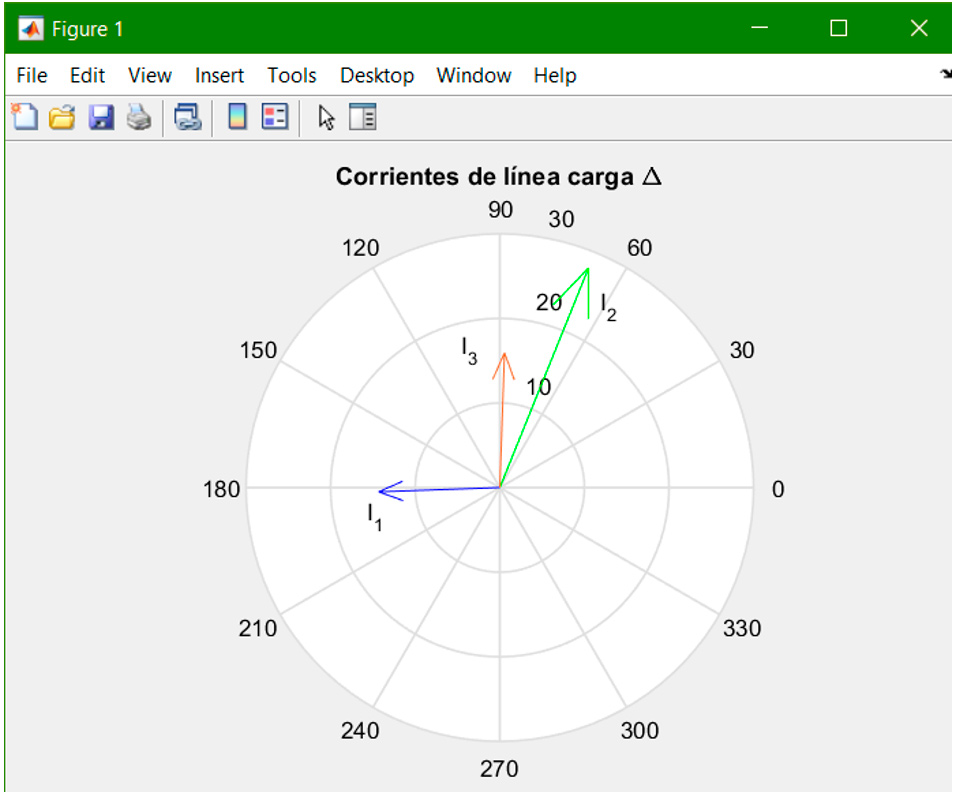
Ejemplo: Graficar los fasores I1 = 14.32∠ − 178°, I2 = 28∠68° e I3 = 15.95∠88°.
Nota: Para asignarles nombres a cada fasor, se usaron cuadros de texto sin línea de borde mediante Insert/Textbox y editando éstos con clic derecho.
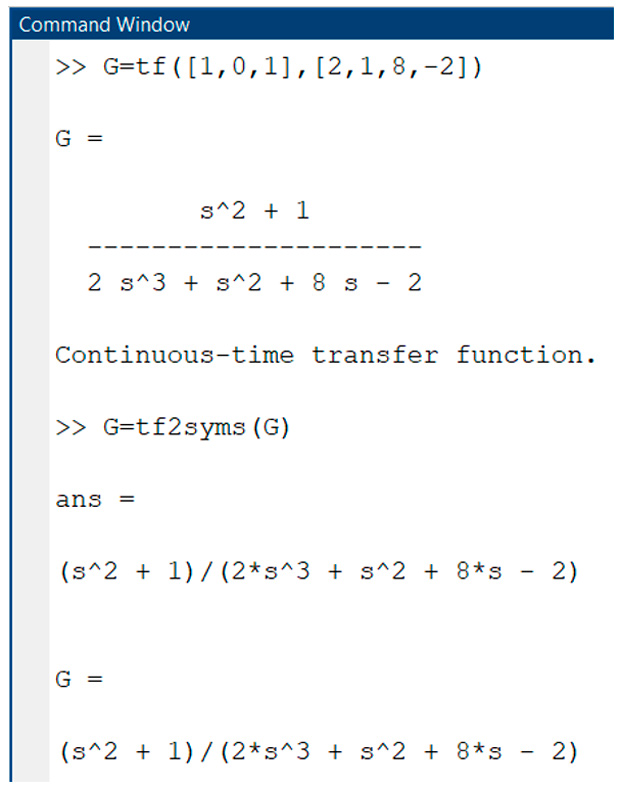
a forma de función de transferencia, lo que permite utilizar funciones como bode, Nyquist, step, etc.
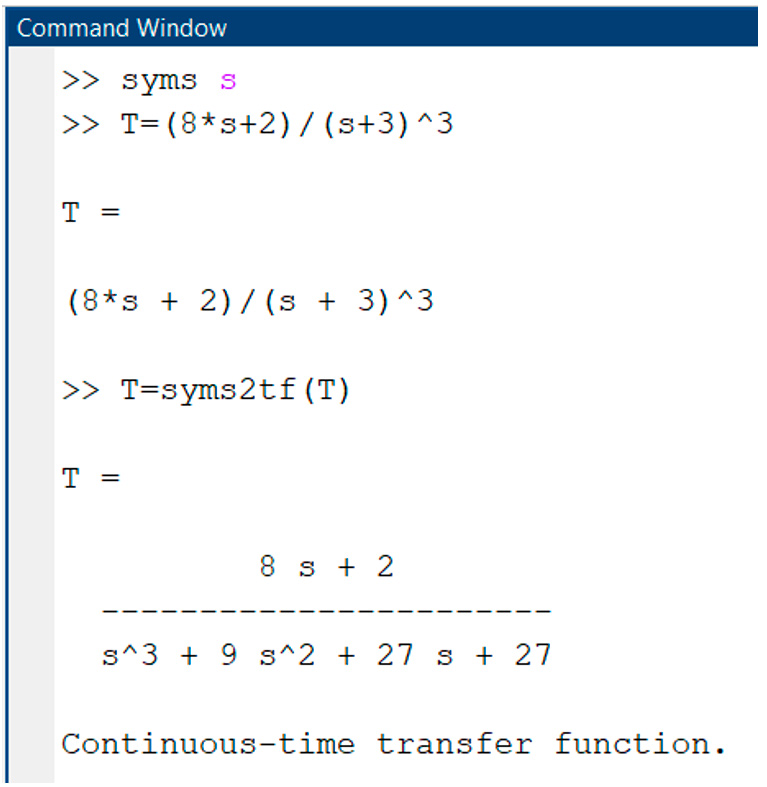
En la figura derecha en cambio, se convierte la función de transferencia
A función simbólica, lo que permite realizar operaciones algebraicas con mayor facilidad.